相关系数的灵感来源，与概率没什么关系，倒是与物理上的电路有一点关系。

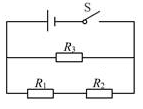
如图所示，电阻\(R_1\)和电阻\(R_2\)串联后，再与电阻\(R_3\)并联。电阻\(R_3\)两端与电阻\(R_1\)和电阻\(R_2\)串联的电路具有相同的电压。如果需要流经电阻\(R_3\)的电流比较大，那么这些电阻之间的阻值应当满足：\(R_3 \le R_1 + R_2 \)。

如果把电阻“类比”成字符串：电阻\(R_i\)对应于字符串\(s_i\)，其电导率\({\sigma _i} = \frac{1}{{{R_i}}}\)对应于字符串的统计词频\(f_i\)。其统计词频\(f_i\)越大，意味着电导率\(\sigma _i\) 越大，电阻\(R_i\)的阻值越小。同等阅读“压力”下（即同等电压下），“电流”就会越大，阅读就会越顺畅。

对于图中的电路，电阻\(R_3\)可以对应于由字符串\(s_1\)和\(s_2\)拼接而成的字符串\(s_3\)。如果字符串\(s_1\)和\(s_2\)有组合成新词汇的倾向，那么电阻\(R_3\)的阻值，就不应当超过串联电路的阻值。由电路并串联规律可知，如果需要流经电阻\(R_3\)的电流比较大，那么这些电阻之间的阻值应当满足：\(R_3 \le R_1 + R_2 \)。

即：\( \frac{1}{{{f_3}}} \le \frac{1}{{{f_1}}} + \frac{1}{{{f_2}}} \)

因此可以定义：

\[ \gamma \propto \frac{{{\sigma _1} + {\sigma _2}}}{{{\sigma _3}}} = \frac{{\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}}}{{\frac{1}{{{f_3}}}}} = {f_3}(\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}) \]

• 实际应用中，会发现其实由字符串\(s_1\)和\(s_2\)拼接而成的字符串\(s_3\)的统计词频\(f_3\)一般是远小于期望值。
• 此时\( \gamma \)的取值范围还与参数个数有一定关系。可以通过除以参数个数（即\( \gamma ^* = \frac{\gamma}{2} \)）将取值范围归一化。

最终可以得到公式：

\[ \gamma = \frac{{{f_3}}}{2}(\frac{1}{{{f_1}}} + \frac{1}{{{f_2}}}) \]

可以通过例举更多电阻串联的情况，就可以得到最终的相关系数公式：

\[ \gamma (s|s_1,s_2,……,s_N) = \frac{f}{N}\sum\limits_{i = 1}^N {\frac{1}{{{f_i}}}} \]

虽然这样得到公式有点牵强附会，不过最终可以通过数学角度分析，得出合理的解释。